編者按

儲能電站作為近年來業界關注的新興業態，在緩解峰荷供電壓力、提供電能備用以及系統的調峰調頻等方面發揮著重要作用。在規劃網側大規模儲能時，需要考慮儲能電站的接入位置是否合適。作為電網中的雙向電力元件，儲能的接入位置能夠直接影響電網潮流分布，改變線路負載并影響網絡損耗和系統的電壓穩定及頻率穩定等。因此，合理選擇儲能電站的接入位置對提高電網系統運行穩定性和安全性尤為重要。

《中國電力》2024年第12期刊發了白望望等撰寫的《基于HC-MOPSO的儲能電站兩階段選址定容方法》一文。文章面向規模化電化學類儲能電站并入網側系統，探討系統靜態電壓穩定性影響機理，構建網側儲能電站選址穩定性評價指標，提出一種將電網系統分區域進行集群的儲能電站選址定容規劃方法。基于有功對電壓的耦合作用，建立二者的靈敏度模型，并基于層次聚類（hierarchical clustering，HC）算法得到電網分區結果，根據靈敏度指標排序選取各分區電壓主導節點作為儲能電站接入點；通過多目標粒子群算法（multi objective particle swarm optimization，MOPSO）對容量配置模型進行求解。最后，以IEEE 39節點系統為例，驗證所提方法的可行性與有效性。

摘要

針對大規模儲能規劃難以兼顧電網有功功率與節點電壓耦合影響的問題，提出一種基于層次聚類（hierarchical clustering，HC）-多目標粒子群（multi objective particle swarm optimization，MOPSO）算法的儲能電站規劃方法。首先，基于系統有功功率與節點電壓間的耦合作用，建立其靈敏度模型，并采用HC算法得到電網區域劃分結果，根據靈敏度指標排序選取各次區域內的電壓主導節點作為儲能電站接入點；其次，以系統靜態電壓穩定裕度最大、總投資與運行成本以及總有功網損最小為目標，建立儲能電站容量配置模型，并設計嵌入潮流計算的MOPSO算法對模型進行求解。最后，以IEEE39節點電力系統網絡為例，驗證所提方法和模型的可行性與有效性。仿真結果表明，本文提出的規劃方法相較于傳統方法可以進一步降低系統有功線損，并提高靜態電壓穩定裕度。

01

電網分區與儲能電站選址

通過在各個分區內選擇電壓控制能力最強的節點，從而簡化電網儲能選址過程，大幅降低優化問題的維數和計算復雜度。此外通過先分區再選址的規劃方法能夠減少儲能電站設備的冗余配置，具體計算流程如圖1所示。

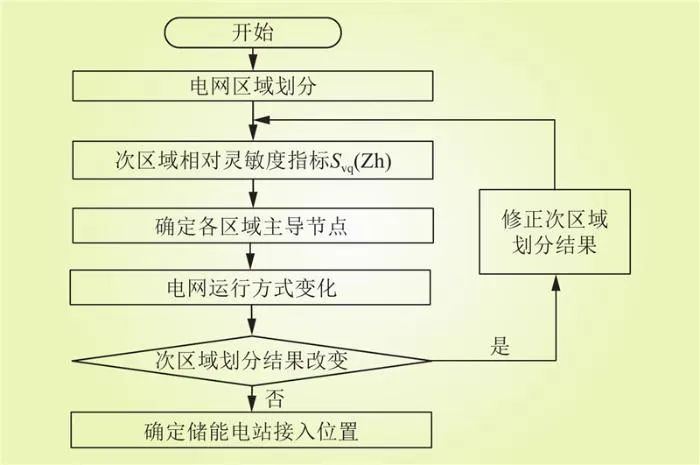
圖1  電網分區與儲能電站選址流程

Fig.1  Grid zoning and site selection process for energy storage power stations

1.1  靈敏度建模

采用牛拉法計算電網潮流得到雅可比矩陣，基于雅可比子矩陣構建含負荷節點的靈敏度矩陣，本文所提方法考慮了有功功率對節點電壓的靈敏度。

基于牛拉法計算雅可比矩陣，可表示為

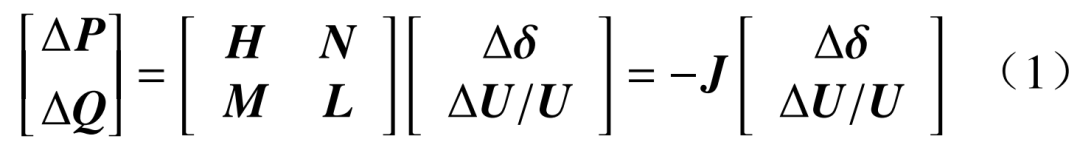
式中：J為潮流雅可比矩陣；?P、?Q分別為有功、無功功率的變化量，由子矩陣H、N、M、L與電壓相角差和幅值變化量?δ、?U/U的乘積得出。

Svq為靈敏度模型，可表示為

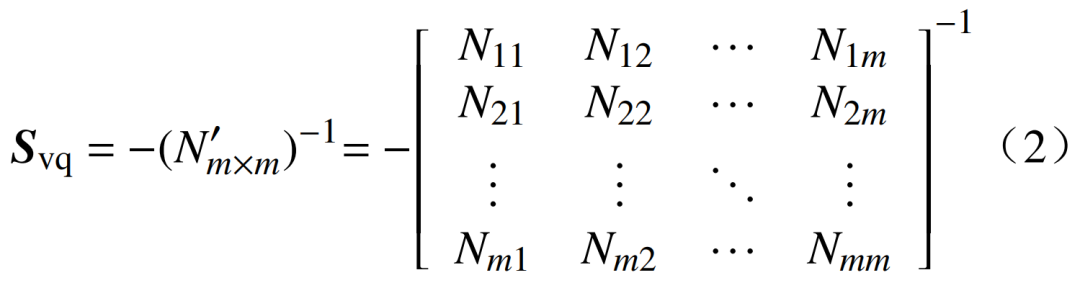
式中：m是負荷節點個數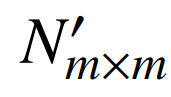；代表子矩陣N中負荷節點的有功-電壓靈敏度，通過有功功率變化量對電壓幅值變化比的偏導數

靈敏度矩陣能夠反映負荷節點i、j之間有功功率對電壓的控制作用，為了衡量節點之間電壓的變化關系，采用i、j之間電壓變化量來表征，即

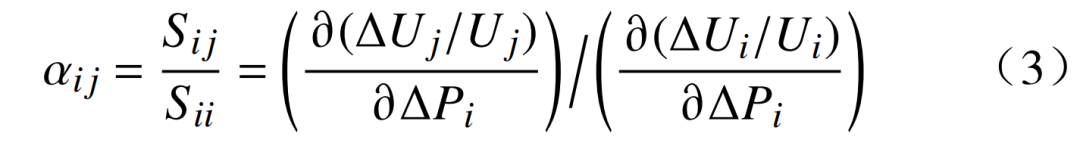
式中：Sij為矩陣Svq中第i行的最大元素，Sii為第i行的其余元素；αij為節點i、j之間的電壓靈敏度，反映了節點j相對于節點i的電壓偏移量。

為了反映節點之間的電氣距離，采用對數函數將節點之間的電壓靈敏度映射到多維空間，形成表征節點區分度的電氣距離矩陣為

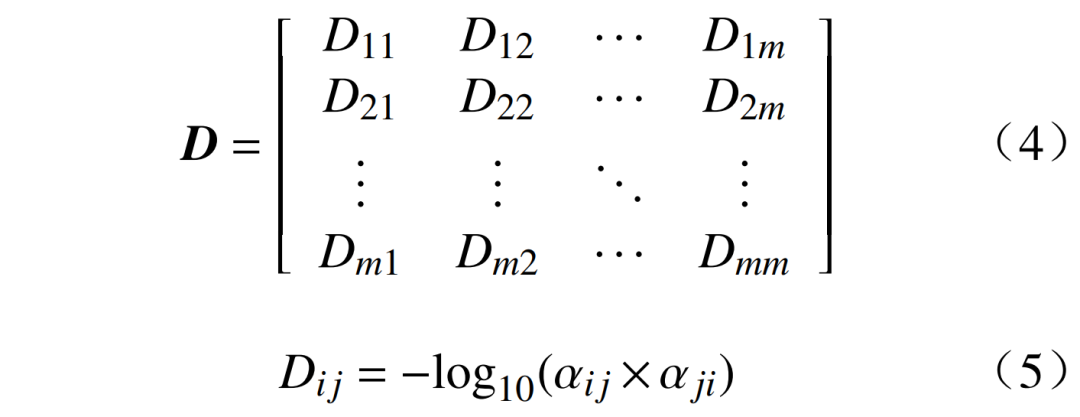
式中：D為負荷節點之間的電氣距離矩陣；Dij為矩陣D中節點i與節點j之間的電氣距離。其中D為對稱矩陣時，Dii的數值為0。

1.2  分區選址模型

聚類算法能夠根據數據集中對象的數字特征將具有相似特征的對象劃分為同一簇，通過衡量數據之間數值特征的相似度進行聚合或區分，以突出不同簇之間的差異。因此，聚類方法可以應用于電網分區研究，通過考慮功率和電壓特性來實現局部電壓控制。

為了確保分區結果均勻準確，基于1.1節中建立的靈敏度和電氣距離矩陣，采用層次聚類法對系統的負荷節點進行劃分，具體步驟如下。1）為減少計算復雜度，本文采用上三角形矩陣Y代替矩陣D，并將Y作為初始合并距離；2）簇之間的相似度度量采用離差平方和（ward）距離方法；3）利用逐級聚類的凝聚過程形成數據集，并構建聚類譜系圖；4）比較聚類譜系中不同分支的區分度大小，確定分區數目，從而得到電網分區結果；5）使用聚類評價信息函數評估聚類結果與實際情況的符合程度。

為了確定儲能電站接入點，采用靈敏度指標辨識電網分區內具有較強電壓控制能力的主導節點，實現分區內部電壓局部控制。以分區內靈敏度為目標，建立的目標函數為

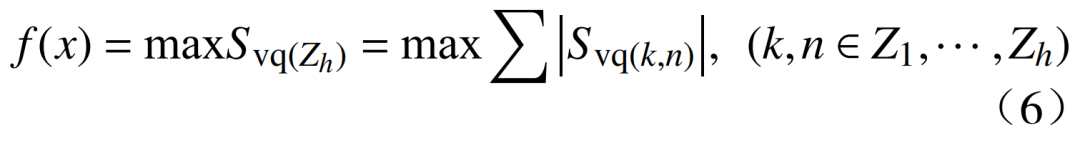
式中：h為劃分的分區編號；Zh為分區h中的節點編號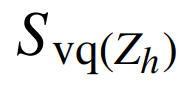；是靈敏度矩陣Svq中在分區h內的節點Zh與分區內所有節點的綜合靈敏度之和；f(x)代表相對于分區內節點靈敏度最高的節點，即電壓主導節點。

02

儲能電站容量配置

綜合考慮靜態電壓穩定裕度、儲能電站投資和運行成本以及總有功網損因素，建立儲能電站容量配置模型，實現各節點儲能電站最佳容量的求解。

2.1  目標函數

儲能電站容量配置模型目標函數包含3部分：節點靜態電壓穩定裕度、儲能電站投資成本與運行成本以及總有功網損。

1）靜態電壓穩定裕度提升系數f1為

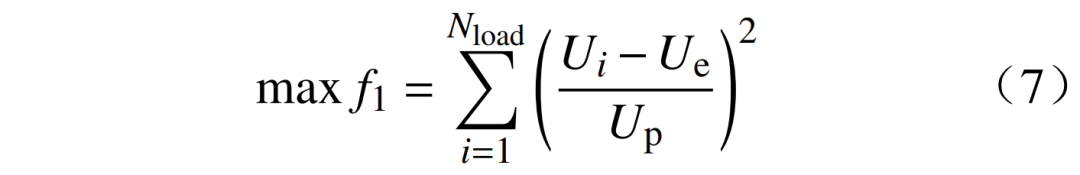
式中：Nload為負荷節點數；Ui為負荷節點電壓值；Ue為節點電壓的期望值；Up為電壓允許偏差。f1的大小反映節點靜態電壓穩定裕度提高的幅度，該值越大，表示儲能電站電壓穩定裕度越高，進而說明選址規劃效果越好。

2）儲能電站投運行成本f2為

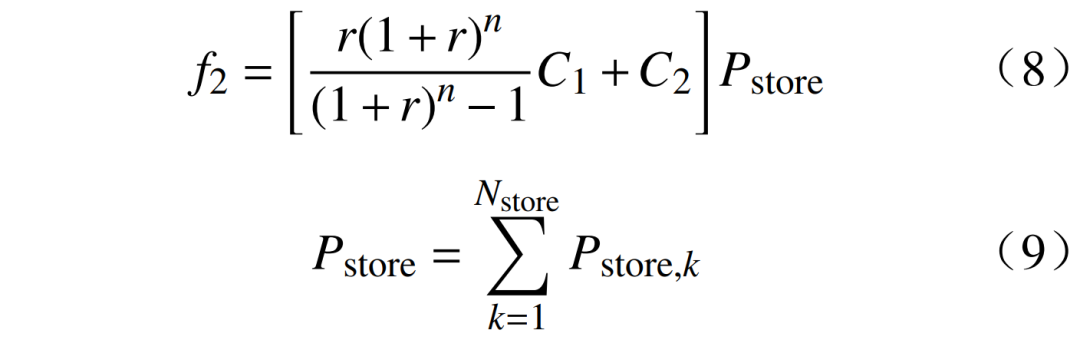
式中：C1和C2分別為儲能電站的投資成本系數和運行成本系數；r為貼現率；n為儲能系統投資回收周期年限；Pstore為儲能電站接入的有功容量；Nstore為系統接入儲能節點數；Pstore,k為儲能電站為k節點提供的有功容量。

3）有功網損。接入儲能系統后，電網在某一時刻的有功網損Ploss為

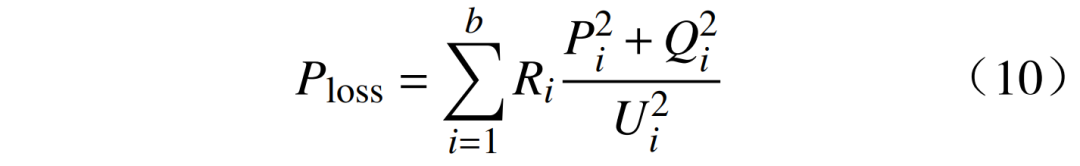
式中：Ri、Pi、Qi分別為支路i的電阻、有功功率、無功功率。

電網系統在一個典型日時段T內總網損表達式f3為

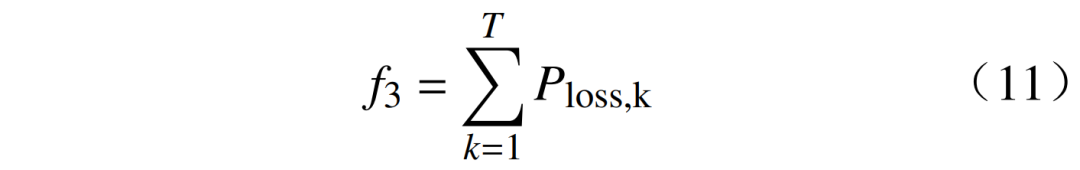
式中：T為總時段數；Ploss,k為系統在k時段內的有功網損。

2.2  約束條件

考慮到系統安全穩定的運行及儲能自身運行狀態限制，具體約束如下。

1）節點電壓約束為

式中：Vmax、Vmin為系統節點電壓上、下限；Vi為節點i的電壓幅值。

2）支路電流約束為

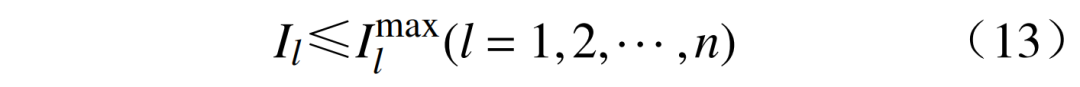
式中：Il為流過線路l的電流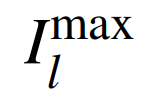；為流過線路l的電流上限；n為總線路數。

3）功率平衡約束為

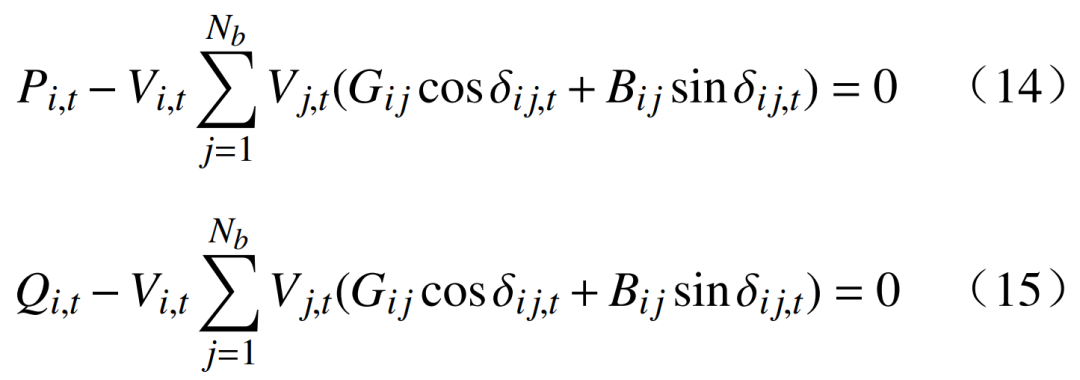
式中：Pi,t和Qi,t分別為在t時刻內注入節點i的有功和無功功率；Gij、Bij、δij,t為節點i和節點j之間的電導、電納和t時刻的電壓相角差；Vi,t、Vj,t為節點i和節點j在t時刻的電壓幅值。

4）儲能功率約束為

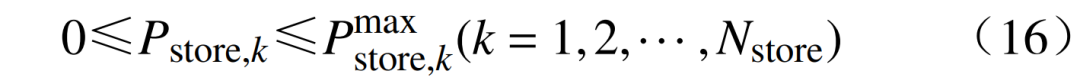
式中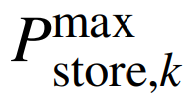：為儲能節點k接入的最大有功容量。

5）儲能數量約束為

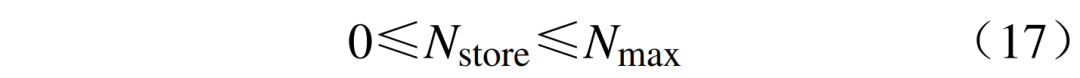
式中：Nstore為儲能安裝數量；Nmax為區內儲能電站最大安裝數量。

2.3  模型求解

根據電網分區以及選址方法選取儲能電站接入電網的最佳節點，并以節點靜態電壓穩定裕度、儲能電站投資和運行成本以及總有功網損作為目標函數，對n個儲能節點的容量進行計算和分析。將不同數量的容量配置結果添加到對應的節點進行PSAT仿真，獲得不同節點不同容量結果下的潮流分布，以靜態電壓穩定裕度提升系數最優為選擇指標，最后得到分區后電網各區域的選址方案以及選址后區內節點的最優容量配置。由于儲能電站容量配置模型中，目標函數包含了多個優化目標，因此選取MOPSO算法求解，算法控制變量即各節點的儲能電站容量。第k次迭代過程中各粒子更新方式為

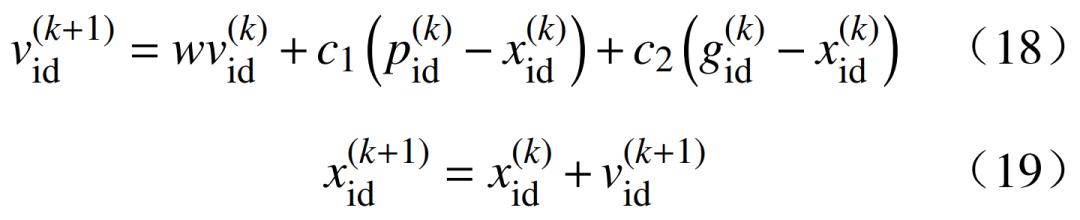
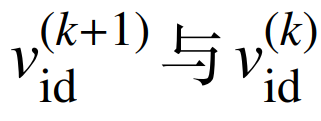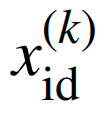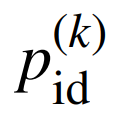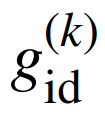式中：分別為第k與k–1次迭代時id粒子的搜索方向；w、c1、c2分別為迭代過程中各部分系數；為id粒子對應的控制變量；與分別為迭代更新過程id粒子獲得的最優解與全局最優解。多個優化目標間通過快速非支配排序得到當前迭代過程的最優解與全局最優解，本文儲能電站容量配置模型求解過程如圖2所示。

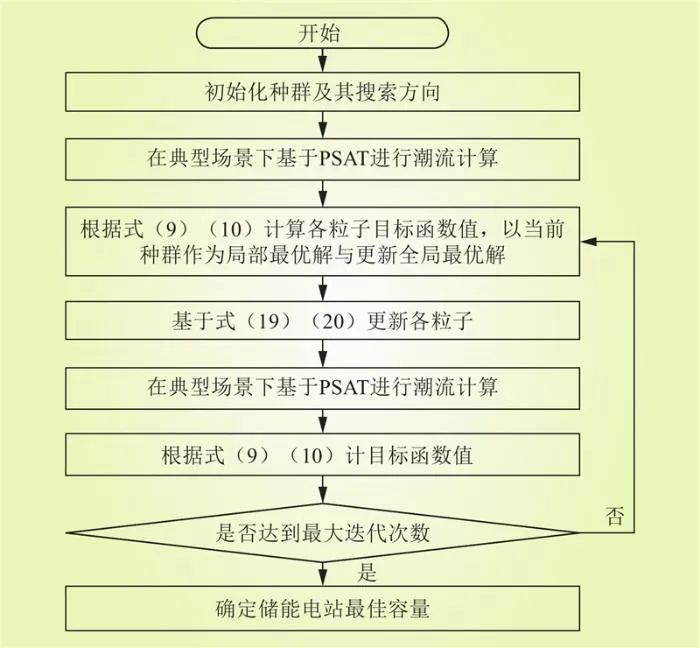
圖2  儲能電站容量配置流程圖

Fig.2  Flow chart of capacity configuration for energy storage power stations

03

算例分析

以標準IEEE 39節點系統為基礎，電網系統拓撲結構如圖3所示，系統中設置10個發電機節點、29個負荷節點、46條支路，其中10條發電機支路和36條負荷支路。

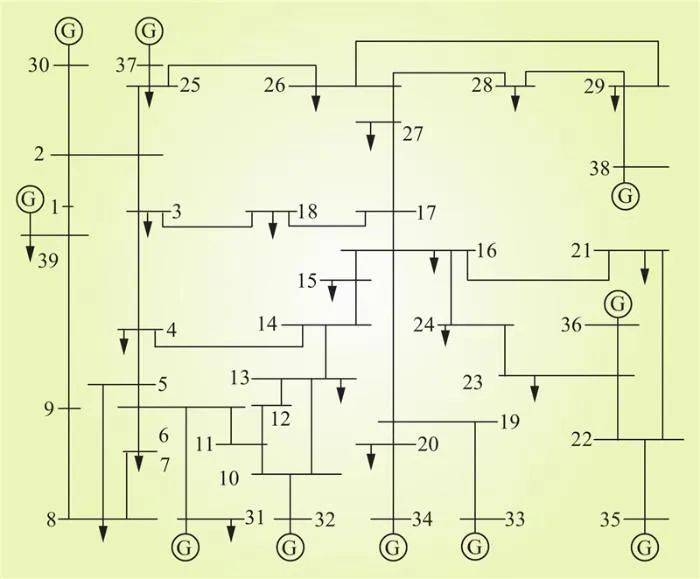
圖3  IEEE 39節點系統拓撲結構

Fig.3  IEEE 39 node system topology

3.1  儲能規劃結果

1）電網分區-選址結果。

電網分區過程中需要對一些特殊節點（如遠離負荷中心的發電機節點）等進行處理。本文在負荷節點分區的基礎上，按照電網拓撲關系采用就近原則對無功源進行就近歸并，從而實現無功資源的合理劃分。根據1.1節所述，基于層次聚類法對電網進行分區，凝聚的聚類譜系圖如圖4所示。由圖4可知，在聚類過程中，當分區數量為6時，區分度最明顯，該位置合并距離為，在此之前節點之間聯系緊密，隨著分區數量的增加，合并距離遞增，由聚類譜系圖可得39節點系統的負荷節點分區結果如表1所示。

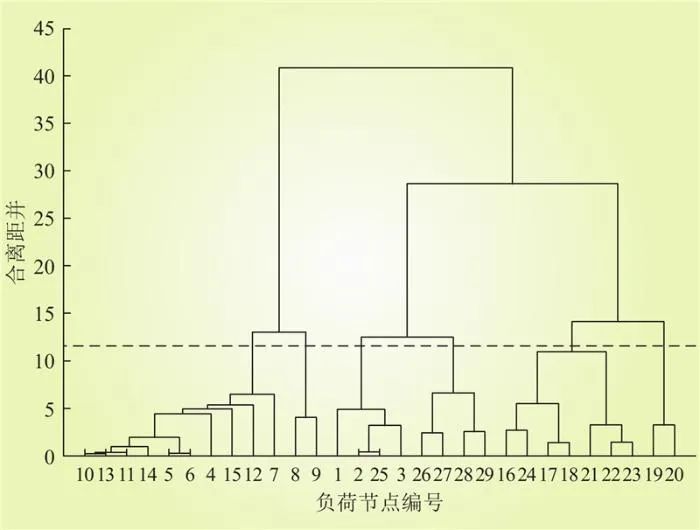
圖4  39節點系統負荷節點聚類譜系

Fig.4  Clustering spectrum of 39-node system load nodes

表1  39節點系統負荷區域劃分結果

Table 1  39 node system load area division results

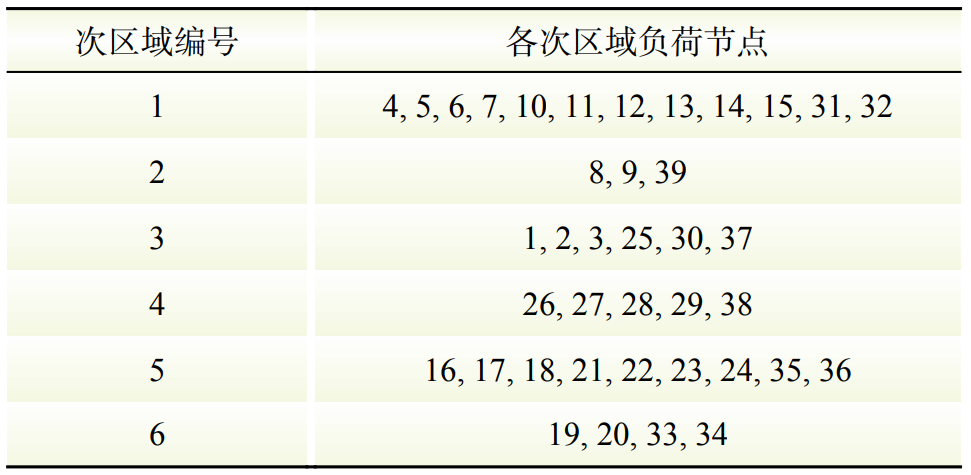
根據1.2節所提電網區域補償點辨識方法，基于靈敏度指標，在不干預無功功率對電壓主控作用的前提下，考慮了有功功率與電壓幅值之間的耦合作用。次區域中的負荷電壓主導節點對該區域中非主導節點的靈敏度反映了其對負荷區域中其他結點的電壓可控性。各次區域相對綜合靈敏度指標計算結果如表2所示。

表2  39節點系統各分區相對靈敏度指標

Table 2  Subregional relative integrated sensitivity metrics for the 39-node system

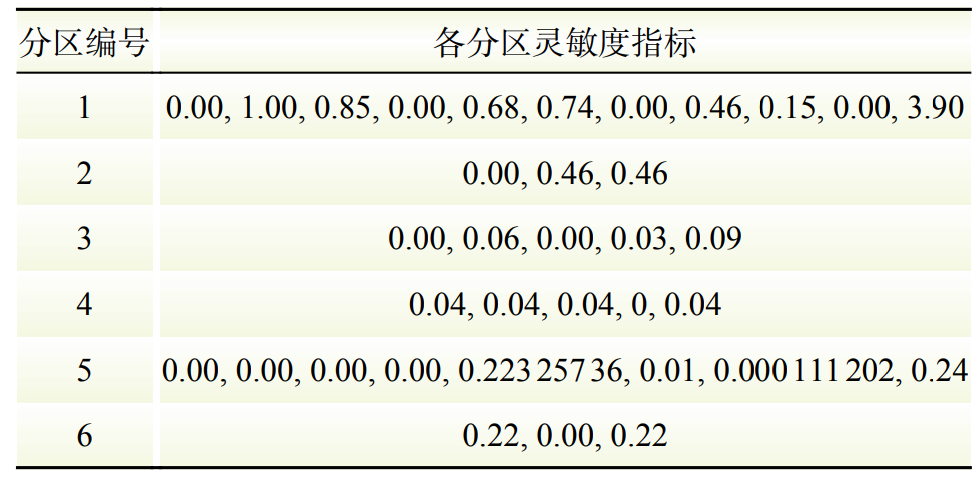
由表2可知，各分區內電壓主導節點為5、9、2、26、22、19。上述電壓主導節點對各自區內的負荷節點起到強控制效果，并且由于在各分區內這些節點的相對靈敏度最大，所以電壓主導節點也能代表各分區內的薄弱環節。電網分區拓撲圖和主導節點選取如圖5所示，由上述結果可知，各次區域的電壓主導節點即為儲能電站最佳接入位置。

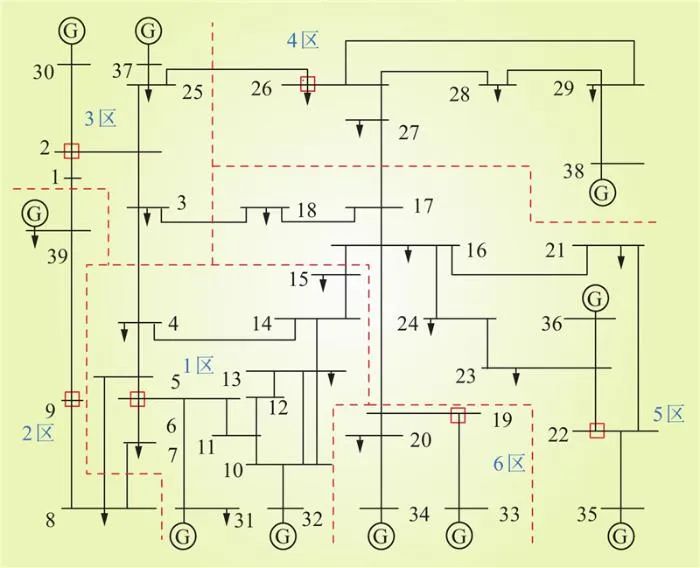
圖5  39節點系統主導節點選取示意

Fig.5  Schematic diagram of the selection of the dominant node of the 39-node system

2）儲能電站容量配置結果。

基于MOPSO算法求解各接入點儲能電站最佳容量，最優解數量設置為20，得到儲能電站容量配置模型的帕累托圖如圖6所示。

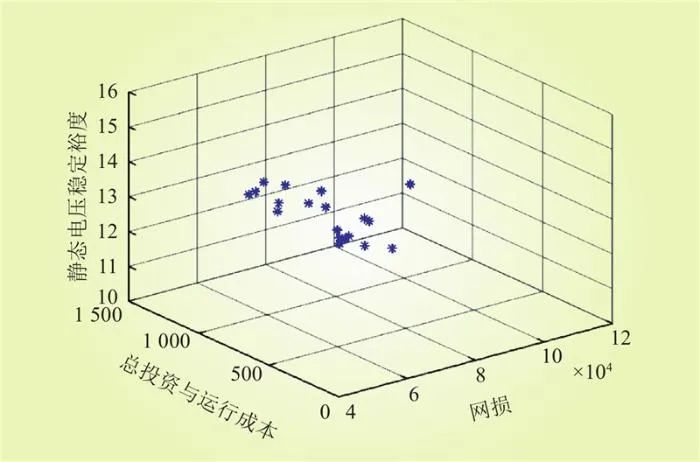
圖6  儲能電站容量配置模型帕累托圖

Fig.6  Pareto diagram of capacity configuration model for energy storage power stations

在所有最優解中，篩選系統總投資成本為60~120億元，靜態電壓穩定裕度大于16，系統總有功線損小于kW，得到3個可行方案，如表3所示。

表3  儲能電站容量可行解

Table 3  Feasible solution for the optimal capacity of energy storage power stations

由表3可見，在儲能電站總容量逐漸增加的過程中，系統的總有功線損逐漸降低，總靜態電壓穩定裕度逐漸升高。其中，方案2相較于方案1，儲能電站總容量增大了10.83 MW，系統的總有功線損降低了kW，系統的靜態電壓穩定裕度升高了1.81。方案3相較于方案2，儲能電站總容量在進一步增大19.53 MW的基礎上，系統的總有功線損降低了kW，系統的靜態電壓穩定裕度升高了3.1，顯著提高了系統的靜態電壓穩定裕度。

3.2  標準條件下不同方案對比

為驗證所提方法的有效性，在標準條件下與文獻[13]所提方法進行對比。基于該文獻的方法，得到IEEE 39節點儲能電站接入節點為21、39，容量大小分別為9 MW、23.9 MW，總投資為63.86億元，系統總有功線損為kW，靜態電壓穩定裕度為14.57。設該文獻得出結果為方案4，4種方案各負荷節點靜態電壓穩定裕度、各線損對比如圖7所示。

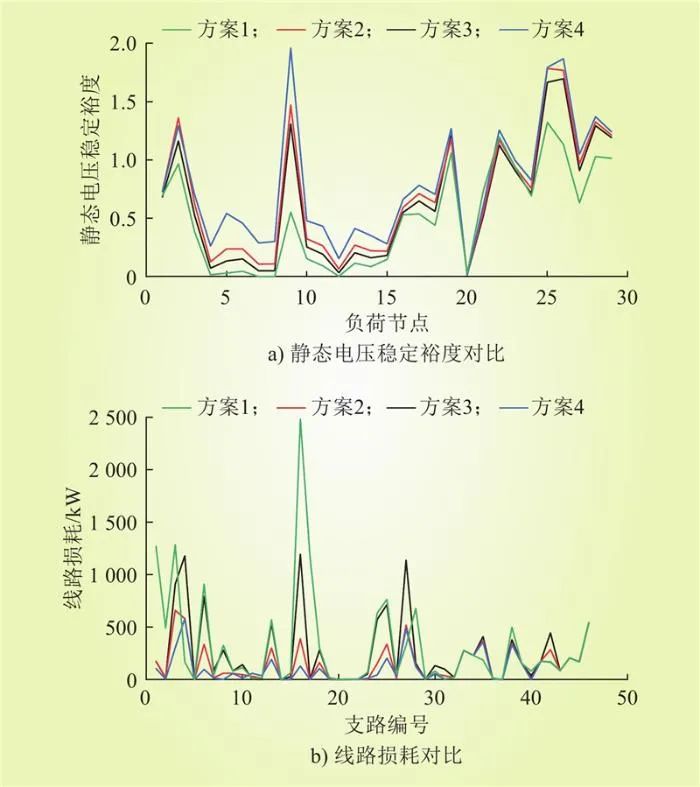
圖7  不同方案系統靜態電壓穩定裕度及線損對比

Fig.7  Comparison diagram of static voltage stability margin and line loss for different schemes of systems

與投資相近的方案1相比，方案4系統的總有功線損要高出kW，而系統的靜態電壓穩定裕度要低3.6。可見，方案1~3在靜態電壓穩定裕度、線路損耗方面均要優于方案4，這是因為先考慮分區再選址的規劃方法，減少了儲能電站設備的冗余配置，且以電網各分區電壓控制能力最強的主導節點作為儲能電站接入點，該方法選取的補償點有助于有功功率優化分布控制。

4種方案在系統投資成本、電壓穩定裕度、總有功線損以及儲能容量等方面的對比如圖8所示，由圖8可見，方案1的4種指標均要優于方案4，方案2雖然配置了更多的儲能容量，但其總有功線損以及電壓穩定裕度均要優于方案4與方案1，因此在選擇具體儲能規劃方案時，可根據實際需求得出相應的帕累托解集。

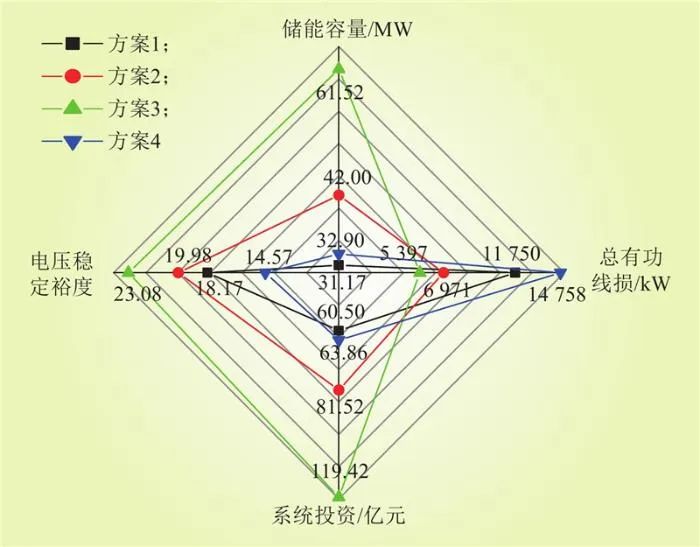
圖8  不同儲能規劃方案對比

Fig.8  Comparison of different energy storage planning schemes

04

結論

針對規模化儲能規劃未能考慮系統靜態電壓穩定性，導致儲能并入電網系統所帶來的經濟效益和安全穩定性難以評估的問題，提出了基于HC-MOPSO的儲能電站兩階段選址定容方法，以IEEE 39節點系統為基礎，與現有儲能電站選址定容方法進行對比分析，主要結論如下。

1）所提儲能電站規劃方法綜合考慮了系統靜態電壓穩定性與經濟效益，極大提升了系統靜態電壓穩定裕度，并降低了網絡損耗。

2）通過先分區再選址的規劃方法，減少了儲能電站設備的冗余配置，降低了系統投資成本，為儲能電站經濟可靠的接入網側提供重要指導。

3）選取電網各分區中電壓控制能力最強的主導節點作為儲能電站的接入點，該方法確定的補償點有助于有功功率優化分布控制，并為系統有功容量規劃提供依據。

在復雜多變的現代電力系統網絡中，規劃儲能電站選址定容工作同樣需要關注系統的暫態穩定以及儲能控制策略等方面的問題，將上述因素納入儲能系統規劃體系，對儲能電站規劃方案進行修正改進，是需要進一步解決的問題。